Wars have always pushed technology in interesting directions. For instance, since conflict began, soldiers have needed to communicate securely on the battlefield. From the dawn of written communication through World War I, codes were made and codes were broken, but people had very little mathematical understanding of information.
During World War II, computer-based encryption took hold. The most famous instance of WW2 cryptography is the German Enigma machine. The Enigma is a keyboard connected to a series of rotors. When you press a key on the keyboard, the series of rotors scramble the output. To descramble the output, you have to know the original configuration of the rotors before the message was typed.
To combat the German Enigma, the Allies were forced to understand the basic mathematics of information. Alan Turing and a team of Allied cryptographers levered seemingly insignificant details -- like Enigma’s inability to encode a letter as itself -- to break the mathematical armor protecting Enigma. While this mathematical battle remained classified for many years, it was recently depicted in two great movies: “Imitation Game” and “Enigma.
Claude Shannon, a U.S. wartime cryptographer who worked for AT&T’s Bell Labs, met Alan Turing when Turing was stationed in Washington, D.C., for two months in 1943. Impressed with and influenced by Turing’s work, by 1944, Claude Shannon had single handedly created a complete theory of information. Shannon’s theories show how to precisely quantify information, determine how much information can travel over a wire, quantify how to ensure that communication is reliable, demonstrate how to compress data, etc. Shannon’s work is incredible, and it certainly has impacted your life more than Einstein’s more famous theories. Without Shannon, for instance, there would be no internet.
By now, you are wondering: “How in the world does this relate to investing?” In 1956, John Kelly, a scientist at AT&T’s Bell Labs, sought to understand noise issues in AT&T’s long-distance telephone signal. While thinking about improving the telephone system, Kelly began thinking about gambling -- a risque subject for a mathematician in the 1950s. One question Kelly asked was: “What would happen if a gambler had a source of useful information, but the source was not always right?”
As an example, consider a gambler in Chicago betting on horse races taking place in New York. This Chicago gambler has a contact in New York who will call him with the results of the race just before betting ends in Chicago. Unfortunately, during an exciting race, the New York crowd can get loud and rowdy. As a result, the Chicago gambler may not be able to understand what his source says, and therefore, he may bet on the wrong horse.
Kelly’s analysis of placing bets with unreliable information came to be known as “The Kelly Criterion.” The Kelly Criterion says that the optimal strategy is to maximize your average return.
To achieve this, you should bet more in cases where you are more likely to win more money, and additionally, you should bet more in cases where you are more certain of the outcomes.
In the professional gambling world, the Kelly Criterion is very important. For example, in blackjack, a good card counter only has a 0.5% advantage over the casino. With such a small edge, it is imperative that a card counter optimally use the available information. By adjusting bet sizes using the Kelly Criterion, a good card counter can improve his edge to roughly 1%.
In his book “The Dhando Investor”, Monish Pabrai gives a clear and concise example from the investing world. For the business Stewart Enterprises, Pabrai estimates the outcomes to be:
I’ll spare you the complicated mathematics involved in calculating the Kelly Criterion. However, what the formula says is, given the above probabilities and expected returns, if an investor has the choice between allocating capital to Stewart Enterprises or allocating capital to cash, the Kelly Criterion indicates that investor should be 97.5% invested in Stewart.
At this point, Pabrai had not heard of the Kelly Criterion, and he invested 10% of his fund’s assets in Stewart Enterprises. If Pabrai had known of Kelly, would he have invested more? Since I know about the Kelly Criterion, would I have invested more than 10%? Maybe not. Here is why.
There are five primary reasons not to bet the full amount suggested by the simple Kelly Criterion. (We can account for these cases using a more complex extension of Kelly’s work.)
1) Opportunity costs. Kelly’s theory says that you should never make investments where there is a probability of total loss for the portfolio. Let’s assume that we can choose between allocating capital to cash, to Stewart Enterprises, and to Trawets Enterprises. Trawets has exactly the same payoff odds as Stewart, and the outcomes of Stewart and Trawets are independent. As a result, if we allocated based on the simple Kelly Criterion, we would invest 97.5% of the portfolio in Stewart and 97.5% of the portfolio in Trawets. Because we have invested almost double our assets, there is a non-zero chance that the portfolio will experience a total loss. As a result, when presented with multiple investment opportunities, the optimal amount to invest in each security is less than the amount that you would invest if the only options were cash and a single security.
2) Overbetting is more harmful than underbetting. If you know the exact probabilities for all outcomes of an investment, then the Kelly Criterion tells you the optimal amount of capital to allocate to the investment. If you allocate slightly less to the investment, you will get a little less return and less volatility. On the other hand, if you invest more than the Kelly Criterion, you will get less return and more volatility -- not a good combination. Furthermore, betting in excess of a certain threshold will guarantee negative expected returns, no matter how favorable each of your individual bets are. In the case of Stewart Enterprises, a bet of 97.5% is optimal. Reducing the bet by 2.5% to 95% will reduce the return and the volatility very slightly. On the other hand, increasing the bet by 2.5% to 100% will almost certainly lead to ruin in the long run, because in 1% of cases, the investment is a total loss.
Keep in mind that the optimal Kelly size is dictated by the actual odds of the problem, rather than what we estimate the odds to be. In cases where there is uncertainty in what the actual odds are, investing a fraction of what Kelly suggests protects us from accidentally overbetting if we have estimated the odds too optimistically.
3) Investing with the full Kelly size results in drawdowns that are beyond the comfort of most investors. By investing a fraction of the Kelly size, the portfolio volatility is easier to stomach, without losing too much return. For instance, in the Stewart Enterprises case, investing full Kelly size results in an average return of 50%, but there always is a 1% chance of losing 97.5% of your portfolio’s value. However, investing half Kelly size results in an average return of 31%, but 1% of the time the maximum loss is only 49%.
4) Infrequent extreme events happen much more frequently than we appreciate. As much as we would prefer not to think about it, extreme events -- like a nuclear weapon detonating in a major city -- do happen, albeit rarely. Because these events are rare and extreme, we inevitably underestimate the odds of them occurring when we compute possible investment outcomes. Again, using a fractional Kelly strategy insulates us from such estimation errors.
5) We may never reach the “long run.” It can be mathematically proven that for fixed goals -- such as multiplying your capital by 100x or 1,000x -- the Kelly investor will reach the goal, on average, in less time than all other strategies. To achieve these results, however, an investor or bettor must be able to make a sufficient number of investments or bets. The catch is that an investor may be unwilling or unable to make enough bets to attain the desired goal with sufficient odds. In such cases, it may be optimal to invest less than what the simple Kelly strategy would suggest.
While many people are familiar with Warren Buffett, very few are familiar with how he actually allocates capital. His approach is clearly at odds with the bulk of the financial industry. Buffett thinks like a Kelly investor. He commonly bets between 25%-40% of his net worth on a single company, and he bets more than that in situations with higher certainty and higher payout. Here is how Buffett described his allocation process:
“I have 2 views on diversification. If you are a professional and have confidence, then I would advocate lots of concentration. For everyone else, if it’s not your game, participate in total diversification. The economy will do fine over time. Make sure you don’t buy at the wrong price or the wrong time. That’s what most people should do, buy a cheap index fund and slowly dollar cost average into it. If you try to be just a little bit smart, spending an hour a week investing, you’re liable to be really dumb.
If it’s your game, diversification doesn’t make sense. It’s crazy to put money into your 20th choice rather than your 1st choice. “Lebron James” analogy. If you have Lebron James on your team, don’t take him out of the game just to make room for someone else. If you have a harem of 40 women, you never really get to know any of them well.
Charlie and I operated mostly with 5 positions. If I were running 50, 100, 200 million, I would have 80% in 5 positions, with 25% for the largest. In 1964 I found a position I was willing to go heavier into, up to 40%. I told investors they could pull their money out. None did. The position was American Express after the Salad Oil Scandal. In 1951 I put the bulk of my net worth into GEICO. Later in 1998, LTCM was in trouble. With the spread between the on-the-run versus off-the-run 30-year Treasury bonds, I would have been willing to put 75% of my portfolio into it. There were various times I would have gone up to 75%, even in the past few years. If it’s your game and you really know your business, you can load up. [...]
In stocks, it’s the only place where when things go on sale, people get unhappy. If I like a business, then it makes sense to buy more at 20 than at 30. If McDonalds reduces the price of hamburgers, I think it’s great.”
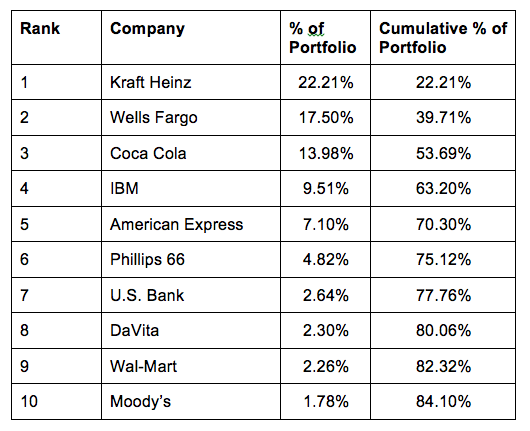
The portfolio of Monish Pabrai (the well-known value investor mentioned earlier) likewise demonstrates Kelly investing.
As this discussion began with information theory, so it will end. The great information theorist Claude Shannon was also a great investor. His long-term return was reported to be 28% per year -- exceeding Buffett’s return for the same period. From the limited information available on Shannon’s portfolio, we know that he would take positions in excess of 80% in a single security. I’m certain that Shannon’s investment ride was extremely bumpy, but he made optimal decisions with the available, uncertain information.
David R. “Chip” Kent IV, PhD
Portfolio Manager / General Partner
Cecropia Capital
Twitter: @chip_kent
Nothing contained in this article constitutes tax, legal or investment advice, nor does it constitute a solicitation or an offer to buy or sell any security or other financial instrument. Such offer may be made only by private placement memorandum or prospectus.